Graphing Quadratic Equations

A quadratic equation is an equation that has a variable to the second power but no variable higher than the second power. A quadratic equation has the form y = ax² + bx + c, where a is not equal to 0.

See an example of a parabola on Wikepedia.

Key points about ax²:

1. Direction of opening: If a > 0, the parabola opens upwards. If a < 0, the parabola opens downwards.

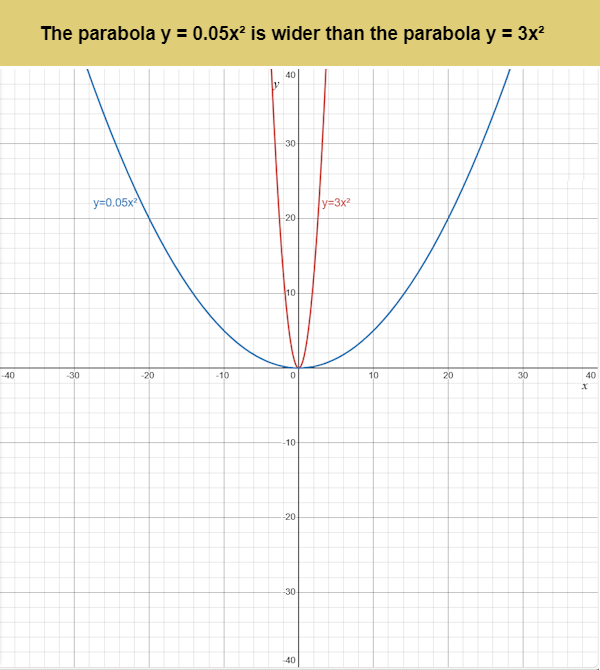
2. Width of the parabola: If |a| > 1, the parabola is narrower. If |a| < 1, the parabola is wider. For example, y = 3x² is narrower than y = 0.5x².

Key Concept of Quadratic Functions:

Parent Function: f(x) = x²
Standard Form: f(x) = ax² + bx + c
Type of Graph: parabola
Axis of Symmetry: \( x = -\frac{b}{2a} \)
y-intercept: c

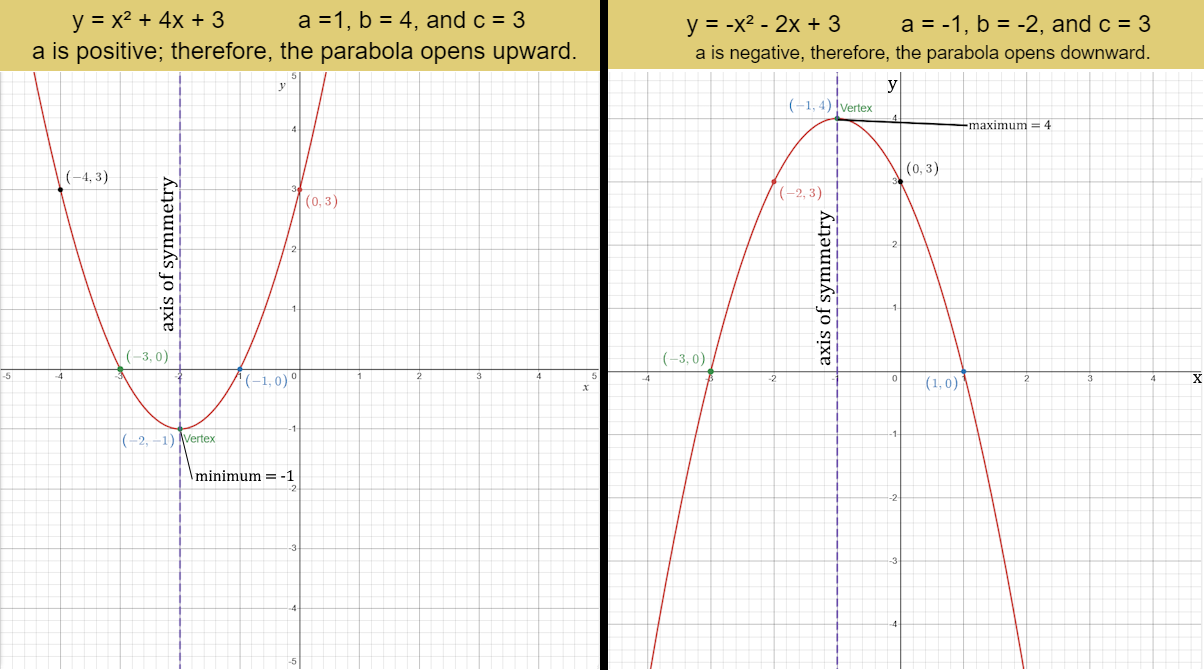
EXAMPLE 1: The graphs of a positive parabola, y = x² + 4x + 3, and a negative parabola, y = -x² - 2x + 3.



The shape of the graph of a quadratic function is called a parabola. Parabolas are symmetric about a central line called the axis of symmetry. The axis of symmetry intersects a parabola at only one point, called the vertex.

In mathematics, a vertex is the point where two lines or curves intersect. The vertex of a parabola is the highest or lowest point.

The maximum value of a parabola is the y-coordinate of the vertex of a parabola that opens downward. The minimum value of a parabola is the y-coordinate of the vertex of a parabola that opens upward. We can identify the minimum or maximum value of a parabola by determining the y-coordinate of the vertex.

Parabolas are symmetrical. This means that if we draw a vertical line down the center of the parabola, the left side and right side would be mirror images of each other. That vertical line is called the axis of symmetry.

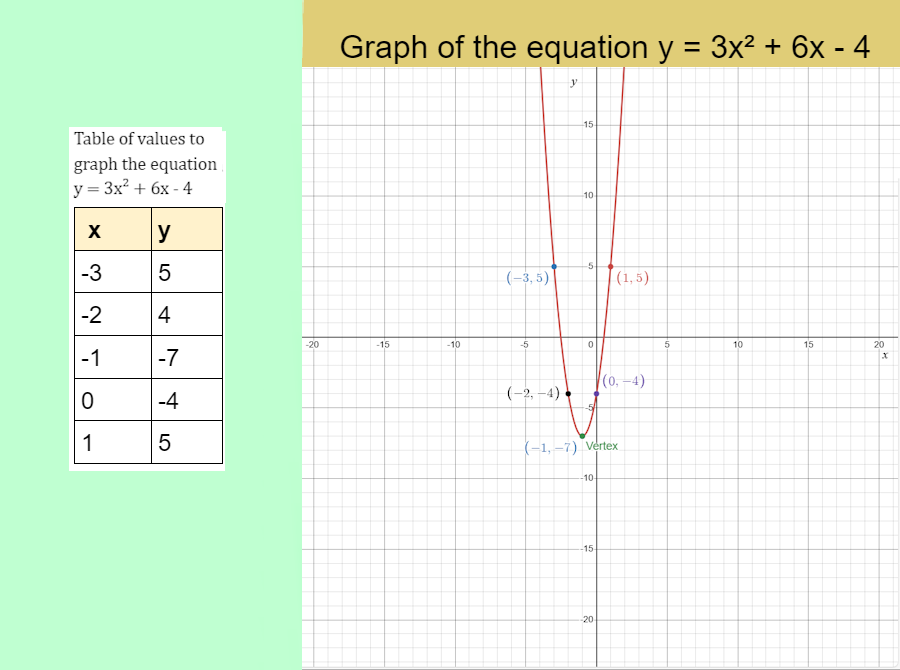
EXAMPLE 2: Graph of a parabola. Use the table of values to graph the equation 3x² + 6x - 4.



EXAMPLE 3:

Find the vertex, axis of symmetry, y-intercept, and minimum or maximum values of the functions y = 2x² + 4x - 1 and y = -x² + 6x + 2.

1.   y = 2x² + 4x - 1     a = 2, b = 4, and c = -1

The axis of the symmetry formula is \( x = -\frac{b}{2a} \)

\( x = -\frac{4}{2(2)} = -1 \)

x = -1 is the axis of symmetry and the x-coordinate of the vertex.

To find the y-coordinate of the vertex, substitute the value for x in the equation y = 2x² + 4x - 1.

y = 2(-1)² + 4(-1) -1 = -3

The vertex is at (-1, -3). Because a is positive, the graph opens up; therefore, the function has a minimum value. a = 2. The minimum value is -3, which is the y-coordinate of the vertex.
The y-intercept always occurs at (0, c). Therefore, the y-intercept is -1.

2.   y = -x² + 6x + 2     a = -1, b = 6, and c = 2

The axis of the symmetry formula is \( x = -\frac{b}{2a} \)

\( x = -\frac{6}{2(-1)} = 3\)

x = 3 is the axis of symmetry and the x-coordinate of the vertex.

To find the y-coordinate of the vertex, substitute the value for x in the equation y = -x² + 6x + 2.

y = -(3)² + 6(3) + 2 = 11

The vertex is at (3, 11). Because a is negative, the graph opens down; therefore, the function has a maximum value. a = -1. The maximum value is 11, which is the y-coordinate of the vertex.
The y-intercept always occurs at (0, c). Therefore, the y-intercept is 2.

Real-World EXAMPLE 1.

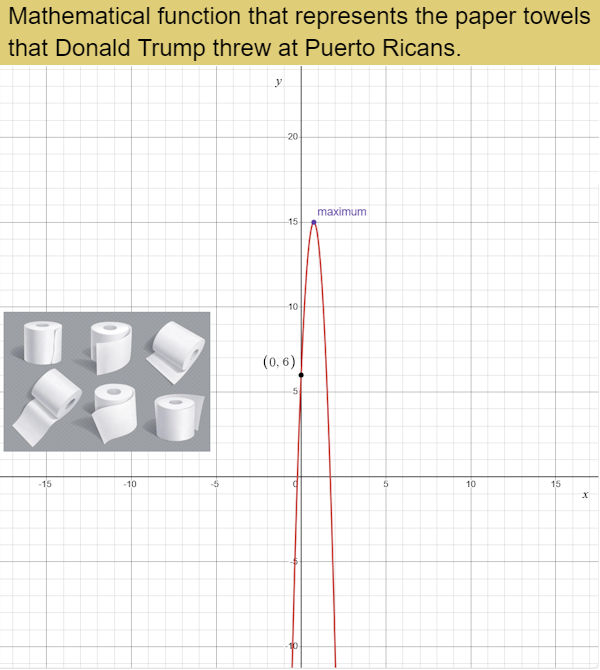
In 2017, Donald Trump threw paper towels into the crowd of hurricane victims in Puerto Rico. The height of the paper towels can be modeled by the function h(x) = -16x² + 24x + 6, where h(x) represents the height in feet of the paper towels after x seconds.

a. Graph the function.

h(x) = -16x² + 24x + 6     a = -16, b = 24, and c = 6

The axis of the symmetry formula is \( x = -\frac{b}{2a} \)

\( x = -\frac{24}{2(-16)} = 3/4 \)

x = 3/4 is the axis of symmetry and the x-coordinate of the vertex.

To find the y-coordinate of the vertex, substitute the value for x in the equation h(x) = -16x² + 24x + 6.

h(x) = -16(3/4)² + 24(3/4) + 6 = 15



b. At what height were the paper towels launched? The paper towels were launched when time equals 0, or at the y-intercept. Therefore, the paper towels were launched at 6 feet from the ground.

c. What is the maximum height of the paper towels? When was the maximum height reached? The maximum height of the paper towels occurs at the vertex. Therefore, the paper towels reach a maximum height of 15 feet. This occurs ¾ or 0.75 seconds after launch.

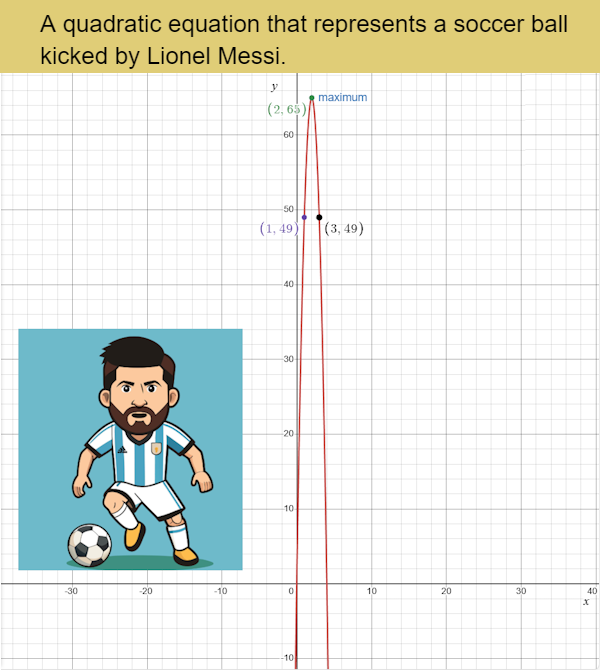
Real-World EXAMPLE 2.

The quadratic equation h = -16t² + 64t + 1 represents the height of a soccer ball in feet after t seconds, if Lionel Messi kicks a soccer ball with an upward velocity of 64 feet per second, and his foot meets the ball 1 foot off the ground. What is the maximum height in feet that the soccer ball reaches?

The equation represents a downward-opening parabola, which is typical for projectile motion.

h = -16t² + 64t + 1     a = -16, b = 64, and c = 1

The axis of the symmetry formula is \( x = -\frac{b}{2a} \)

\( x = -\frac{64}{2(-16)} = 2 \)

x = 2 is the axis of symmetry and the x-coordinate of the vertex.

To find the y-coordinate of the vertex, substitute the value for x in the equation h = -16t² + 64t + 1.

h = -16(2)² + 64(2) + 1 = 65

The maximum height of the soccer ball occurs at the vertex. Therefore, the soccer ball reaches a maximum height of 65 feet. This occurs 2 seconds after the soccer ball was kicked. In 3 seconds, the soccer ball is returning to the ground and is at a height of 49 feet.